Teoría Geometría Analitica

Geometría Analítica:

http://filosofia.laguia2000.com/wp-content/uploads/2010/02/Descartes-Ren%C3%A9-Segunda-Parte.gif

Esta geometría es la unión del algebraica (expresiones algebraicas) y la geometría euclidiana,  las cuales se pueden representar en  "el plano Cartesaino" desarrollado por el matemático y filosofo Rene Descartes, por medio coordenadas.

En el plano cartesiano encontramos los ejes  y (ordenadas)
y  eje x  (abscisas) . en el cual podemos representar diferentes figuras geométricas por medio de funciones:

Función lineal 

"Una función lineal es una función polinomica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:

f(x) = mx + b

donde m y b son constantes reales y x es una variable real." (wikipedia s.f)

Función cuadrática

Funciones trigonométricas

Las funciones trigonométricas se definen como el cociente entre dos lados de un triángulo rectángulo y sus ángulos. De esta forma:

Función Seno: Es la división entre el cateto opuesto y la hipotenusa.

• Período: 2𝛑
• Amplitud: 1
• Raíces: k𝛑 (k es un número entero).

Función Coseno: Es el cociente entre el cateto adyacente y la hipotenusa.

• Período: 2𝛑
• Amplitud: 1
• Raíces: 𝛑/2 + k𝛑 (k es un número entero)

Función Tangente: Es la relación entre el cateto opuesto y el cateto adyacente, es decir entre las funciones seno y coseno.

• Período: 𝛑
• Amplitud: Infinita.
• Raíces: k𝛑 (k es un número entero).

Además están las funciones que son las inversas multiplicativas de las anteriormente mencionadas:

Función Cosecante: Es la inversa multiplicativa de la Función Seno.

• Período: 2𝛑
• Amplitud: Infinita.
• Raíces: No tiene.

Función Secante: Es la inversa multiplicativa del Coseno.

• Período: 2𝛑
• Amplitud: Infinita.
• Raíces: No tiene.

Función Cotangente: Es la inversa multiplicativa de la Tangente.

• Período: 𝛑
• Amplitud: Infinita.
• Raíces: 𝝅/2 + k𝝅 (k es un número entero).

Cómo graficar las funciones trigonométricas? El siguiente vídeo muestra dos métodos muy útiles para realizar dichas gráficas:

Disponible en: https://www.youtube.com/watch?v=n6857q5hM5E

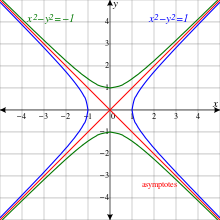
Sección de cónicas

¿Qué es una cónica?

Se define como: “El conjunto de puntos en el plano para los cuales la razón entre la distancia de los mismos a un punto (llamado FOCO) y la distancia a una recta (llamada DIRECTRIZ) dan una constante (llamada “e” EXCENTRICIDAD)

Vamos a verlo de otra manera:

Hay tres tipos de curvas que cumplen con la condición de las cónicas

* Parábola                   *  Hipérbola               * Elipse

                              

Una de las grandes diferencias entre ellas es el valor de su “Excentricidad”

Referencias Bibliográficas

• Wikipedia, Geometría analítica. Recuperado de: https://es.wikipedia.org/wiki/Geometría_analítica
• Wikipedia, Función lineal. Recuperado de: https://es.wikipedia.org/wiki/Función_lineal
•  Wikipedia,  Función cuadrática. Recuperado de: https://es.wikipedia.org/wiki/Función_cuadrática
• Ediciones logikamente. Libro de matematicas a medida. Cónicas. Recuperado de: http://www.logikamente.com.ar/?page=Recursos::Los_84_temas. 
• Wikipedia. Función Trigonometrica. Disponible en: https://es.wikipedia.org/wiki/Funci%C3%B3n_trigonom%C3%A9trica